|
"Нахождение градусных мер углов в треугольнике (сумма углов треугольника, свойство внешнего угла трегольника, биссектриса, высота)"
|
!!! В текстовое поле запишите целое число или десятичную дробь. Целую и дробную часть отделяйте запятой.
!!! Для просмотра правильного решения встроена интерактивная презентация или видеоролик с разбором решений. 
Встроенная интерактивная презентация работает, как и презентация Power Point. Анимация осуществляется щелчками по триггеру "Смайлик" . |
Опорный конспект
|
 Теорема. Сумма углов треугольника равна 180°.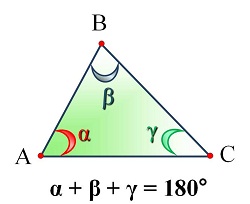 
|
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Теорема. Внешний угол треугольника равен сумме двух других углов, не смежных с ним.
|
Теорема. Сумма острых углов прямоугольного треугольника равна 90°.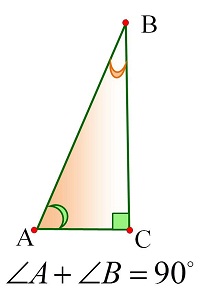
|
Теорема. Каждая сторона треугольника меньше суммы двух других сторон ( неравенство треугольник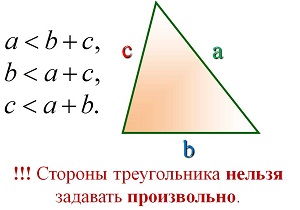а).
|
Теорема. В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.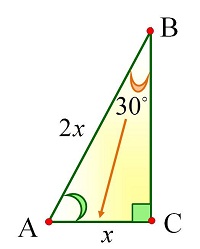
|
Памятка для составления уравнения |
| Один на 32 больше другого. |
|
Один: x + 32, другой: x. |
или |
Один: x, другой: x - 32. | |
| Один на 32 меньше другого. |
|
Один: x, другой: x + 32. |
или |
Один: x - 32, другой: x. | |
| Один относится к другому как 3:2. |
|
| Один в 32 раза больше другого. |
|
Один: 32x, другой: x. |
или |
Один: x, другой: x/32. | |
| Один в 32 раза меньше другого. |
|
Один: x, другой: 32x. |
или |
Один: x/32, другой: x. | |
|
Тест с разбором решений |
1-7
|
